Spacier

はじめに

Spacierは特に高分子の分野における分子空間データのデータ探索と解析のためのツールを提供するPythonパッケージです。このレビューでは、インストールから基本的なポリマーの探索の実行までをレビューします。

使用環境

今回のレビューにおける使用環境は以下のとおりです。

• Mac OS
• Python 3.13

インストール・コンパイル方法

（必要に応じて）pythonの仮想環境を作成、起動します。

python3 -m venv venv
cd venv
source bin/activate

SpacierのGitリポジトリをクローンします。

git clone https://github.com/s-nanjo/Spacier.git

最後に必須環境と、あとで使うオプションのライブラリ(matplotlib)をインストールをします。

cd Spacier
pip install .
pip install matplotlib

以上で基本的なライブラリのインストールは完了です。

最後に一応バージョンの確認をしておきます。

python
import sys
sys.path.append('../lib/python3.13/site-packages/')
from spacier.ml import spacier

print("spacier: ", spacier.__version__)

出力は spacier: 0.0.5 でした。

ポリマーの探索

examples ディレクトリの 1_Experiments.ipynb に従い、いくつかの目的におけるポリマーの探索と、それに関する最適化の具体例を見ていきます。その準備として以下のファイルを用意します:

# python: prep.py
import sys
sys.path.append('../lib/python3.13/site-packages/')
from spacier.ml import spacier
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

def load_datasets():
    data_path = "./spacier/data"
    df_X = pd.read_csv(f"{data_path}/X.csv")          # training data
    df_pool_X = pd.read_csv(f"{data_path}/X_pool.csv")  # pool of candidates

    df = pd.read_csv(f"{data_path}/y.csv")            # known outcomes
    df_oracle = pd.read_csv(f"{data_path}/y_oracle.csv")   # oracle or ground truth data
    
    return df_X, df_pool_X, df, df_oracle

def update_datasets(df_X, df_pool_X, df, df_oracle, new_indices):
    # Update df_X by adding selected rows from df_pool_X and reset index
    df_X = pd.concat([df_X, df_pool_X.iloc[new_indices]]).reset_index(drop=True)
    
    # Remove the selected rows from df_pool_X and reset index
    df_pool_X = df_pool_X.drop(new_indices).reset_index(drop=True)
    
    # Directly add selected rows from df_oracle to df and reset index
    df = pd.concat([df, df_oracle.iloc[new_indices]]).reset_index(drop=True)

    # Remove the selected rows from df_oracle and reset index
    df_oracle = df_oracle.drop(new_indices).reset_index(drop=True)

    return df_X, df_pool_X, df, df_oracle

load_datasets() はSpacierのサンプルデータセットを読み込みます。
update_datasets() はサンプル new_indices を新たに選んだあとの探索手法に寄らない部分の作業をし、もう一度サンプルを選ぶ準備をします。

実験1: 高熱伝導率のポリマーの探索

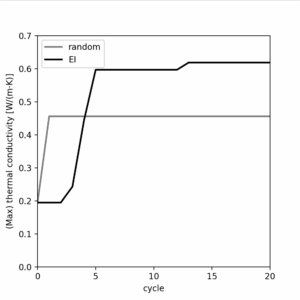
まずは特定の性質について優れたポリマーを探索する方法を見ていきます。今回は、高い熱伝導率を持つポリマーを期待改善量(EI)の方法を用いて探索し、ランダムサンプリングとパフォーマンスを比較します。

# python: Experiment-1.py
from prep import *  # load the file prepared above

# Expected Improvement (EI)
df_X, df_pool_X, df, df_oracle = load_datasets()
highest_value_ei = [df["thermal_conductivity"].max()]

for num in range(20):
    new_index = spacier.BO(df_X, df, df_pool_X, "sklearn_GP",
                           ["thermal_conductivity"]).EI(10)
    df_X, df_pool_X, df, df_oracle = update_datasets(
        df_X, df_pool_X, df, df_oracle, new_index)
    highest_value_ei.append(df["thermal_conductivity"].max())

# Random sampling
df_X, df_pool_X, df, df_oracle = load_datasets()
highest_value_random = [df["thermal_conductivity"].max()]

for num in range(20):
    new_index = spacier.Random(df_X, df_pool_X, df).sample(10)
    df_X, df_pool_X, df, df_oracle = update_datasets(
        df_X, df_pool_X, df, df_oracle, new_index)
    highest_value_random.append(df["thermal_conductivity"].max())

# plot
plt.figure(figsize=(4, 4))
plt.xlim(0, 20)
plt.ylim(0, 0.7)
plt.xlabel("cycle")
plt.ylabel(r"(Max) thermal conductivity [W/(m$\cdot$K)]")
plt.xticks(np.arange(0, 21, 5))
plt.plot(np.arange(0, 21), highest_value_random,
         label="random", color="grey", lw=2)
plt.plot(np.arange(0, 21), highest_value_ei,
         label="EI", color="k", lw=2)

plt.legend()
plt.show()

最後のプロットは各サンプリングのサイクルで最も高い熱伝導率を持つポリマーを出力するものです。さて、これを実行しましょう。

python3 Experiment-1.py

10秒ほどすると以下のようなプロットが出力されました。

実験2: 特定の性質を持つポリマーの探索

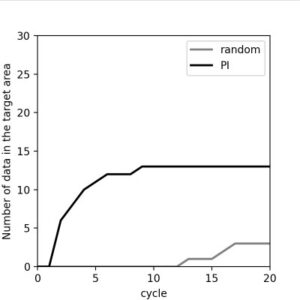
次に条件を満たすポリマーの探索方法を見ていきます。今回は比熱容量が3000–4000、屈折率が1.6–1.7、密度が1.0–1.1のポリマーを、改善量確率(PI)の方法を用いて探索し、ランダムサンプリングとパフォーマンスを比較します。

# python: Experiment-2.py
from prep import *

# Probability of Improvement (PI)
df_X, df_pool_X, df, df_oracle = load_datasets()
hit_pi = [0]

properties_to_update = ["Cp", "refractive_index", "density"]

for num in range(20):
    new_index = spacier.BO(df_X, df, df_pool_X, "sklearn_GP",
                           properties_to_update).PI(
        [[3000, 4000], [1.6, 1.7], [1, 1.1]], 10)
    df_X, df_pool_X, df, df_oracle = update_datasets(
        df_X, df_pool_X, df, df_oracle, new_index)
    hit_pi.append(len(df.query(
        "3000 < Cp < 4000 and 1.6 < refractive_index < 1.7 and 1 < density < 1.1")))

# Random Sampling
df_X, df_pool_X, df, df_oracle = load_datasets()
hit_random = [0]

for num in range(20):
    new_index = spacier.Random(df_X, df_pool_X, df).sample(10)
    df_X, df_pool_X, df, df_oracle = update_datasets(
        df_X, df_pool_X, df, df_oracle, new_index)
    hit_random.append(len(df.query(
        "3000 < Cp < 4000 and 1.6 < refractive_index < 1.7 and 1 < density < 1.1")))

# plot
plt.figure(figsize=(4, 4))
plt.xlim(0, 20)
plt.ylim(0, 30)
plt.xlabel("cycle")
plt.ylabel("Number of data in the target area")
plt.xticks(np.arange(0, 21, 5))
plt.yticks(np.arange(0, 31, 5))
plt.plot(np.arange(0, 21), hit_random,
         label="random", color="grey", lw=2)
plt.plot(np.arange(0, 21), hit_pi,
         label="PI", color="k", lw=2)
plt.legend()
plt.show()

最後のプロットは各サンプリングのサイクルまでに探索できた条件を満たすポリマーの数の累計です。実行すると10秒ほどで完了し、プロットは以下のようになりました。

実験3: パレート曲面探索

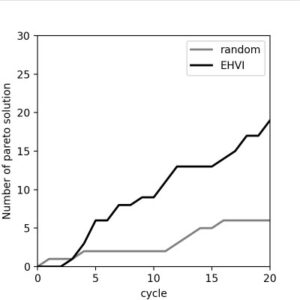
最後にポリマーの複数の性質について優れているものを探索します。多くの場合トレードオフとなるのである程度「妥協」をすることになりますが、少なくとも上位互換が無いポリマーが望ましいです。このようなデータをパレート解と呼びます。今回は比熱容量と屈折率について、そのパレート解を期待超体積改善量(EHVI)の方法を用いて探索します。

# python: Experiment-3.py
from prep import *

# Identifying the Pareto Front
df_X, df_pool_X, df, df_oracle = load_datasets()
PF = spacier.PF_max(df_oracle["Cp"].values,
                    df_oracle["refractive_index"].values)
PF_idx = []
for num in range(len(PF)):
    prop1 = PF[num][0]
    prop2 = PF[num][1]
    tmp = (df_oracle["Cp"] - prop1).abs() + \
          (df_oracle["refractive_index"] - prop2).abs()
    index = df_oracle.index[tmp.argsort()][0].tolist()
    PF_idx.append(df_oracle.iloc[index]["monomer_ID"])

# Expected Hypervolume Improvement (EHVI)
df_X, df_pool_X, df, df_oracle = load_datasets()
hit_ehvi = [0]

properties_to_update = ["Cp", "refractive_index"]

for num in range(20):
    new_index = spacier.BO(df_X, df, df_pool_X, "sklearn_GP",
                           properties_to_update,
                           standardization=True).EHVI(10)
    df_X, df_pool_X, df, df_oracle = update_datasets(
        df_X, df_pool_X, df, df_oracle, new_index)
    hit_ehvi.append(len(set(list(df["monomer_ID"])) & set(PF_idx)))

# Random Sampling
df_X, df_pool_X, df, df_oracle = load_datasets()
hit_random = [0]

for num in range(20):
    new_index = spacier.Random(df_X, df_pool_X, df).sample(10)
    df_X, df_pool_X, df, df_oracle = update_datasets(
        df_X, df_pool_X, df, df_oracle, new_index)
    hit_random.append(len(set(list(df["monomer_ID"])) & set(PF_idx)))

# plot
plt.figure(figsize=(4, 4))
plt.xlim(0, 20)
plt.ylim(0, 30)
plt.xlabel("cycle")
plt.ylabel("Number of pareto solution")
plt.xticks(np.arange(0, 21, 5))
plt.yticks(np.arange(0, 31, 5))
plt.plot(np.arange(0, 21), hit_random,
         label="random", color="grey", lw=2)
plt.plot(np.arange(0, 21), hit_ehvi,
         label="EHVI", color="k", lw=2)
plt.legend()
plt.show()

最後のプロットは各サンプリングのサイクルまでに探索できたパレート解の数の累計です。実行すると3分ほどで完了し、プロットは以下のようになりました。

終わりに

ということで、Spacierのインストールから基本的な探索の方法をレビューしました。またどの探索手法でも、一定の回数を繰り返すとランダムサンプリングよりは高いパフォーマンスを示すことがわかりました。
他の機能の紹介は examples ディレクトリにあるので、そちらを参照してみてください。