田村亮(物質・材料研究機構)吉見一慶(東京大学物性研究所)
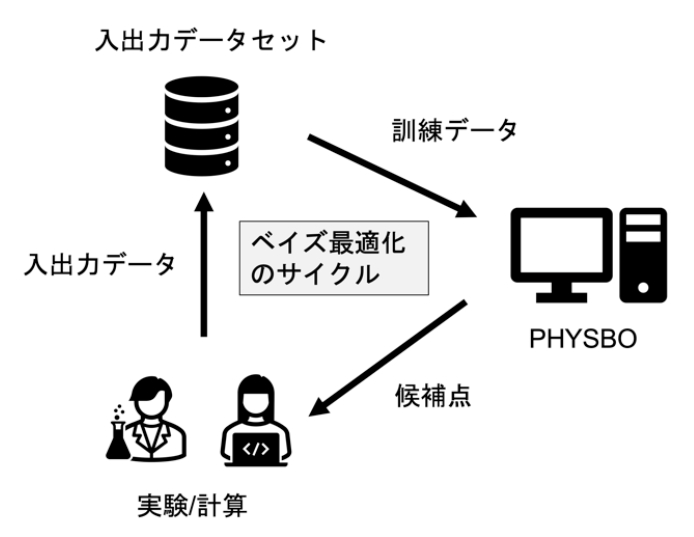
図1: ベイズ最適化のサイクル
研究のポイント(着眼点)
- 欲しい物性を持った物質を探すことは、物性を調べることに比べはるかに難しい。
- ベイズ最適化を用いることで、所望の物性を持つと予想される物質の組成や合成パラメータを機械学習から提案を受けることができる。しかし、パラメータ数が多くなるとベイズ最適化を実施するためのスコア計算に時間がかかる。
- 上記の問題を解決するために、スコア計算に関して高並列計算が可能なPythonライブラリPHYSBOを開発した。
ツールへのリンク
用語
ベイズ最適化
概要
所望の物性から組成や合成パラメータを導く最適化問題は、一般的に与えられた組成やパラメータから物性を導く事より難しい問題となる。これは広い範囲の組成やパラメータに対して計算または実験を実施する必要があるためである。このような最適化問題に対して用いられる手法にベイズ最適化と呼ばれるものがある。ベイズ最適化にもパラメータが増える事で計算量が多くなるという問題点があり、本事例で挙げるPHYSBOは並列化を用いる事でこの問題に対応している。
研究の背景
物質の組成やパラメータが与えられると、その物性は実験、計算で求める事が可能である。これに対して、物性研究では逆に欲しい物性から組成、パラメータ等を求めたいニーズがある。これは広いパラメータ空間内で最適な値を選ぶ事になるため、難しい問題である。もっとも単純には全てのパラメータにおいて実験あるいは計算を実施し、結果を比較すれば良いが、これはパラメータ数が増えると実質的には不可能である。また、ランダムに候補点を抽出して基準を満たすパラメータを探索する事も出来るが、これも非効率である。
このような問題に対して、ベイズ最適化と呼ばれる手法を用いる事で効率的に組成やパラメータの候補点を抽出する事が可能である。これは、これまで取得したデータから、機械学習によって、まだ実験・計算をしていない組成やパラメータに対して予測値と不確かさを見積り、候補点にスコアを付け、最もスコアの良いものを次の実験・計算の対象とするものである。このスコア付けによってより少ない候補点で基準を満たす組成やパラメータを見つける事が可能となる。
ベイズ最適化によって、より少ない回数で最適化問題を解く事が可能になったものの、これを実施するためには各ステップで全ての候補点に対してスコアを付ける必要があるためパラメータが多くなるとその数に比例して計算量が多くなるという問題がある。PHYSBO (optimization tool for PHYSics based on Bayesian Optimization)はPython2で開発されていたベイズ最適化ライブラリCOMBO (COMmon Bayesian Optimization Library)を元に、Python3に対応すると共にスパコン等の高並列環境に対応させたライブラリである。これにより、スーパーコンピュータ等を用いる事で、計算量が多かったスコア計算を高速化している。
このような問題に対して、ベイズ最適化と呼ばれる手法を用いる事で効率的に組成やパラメータの候補点を抽出する事が可能である。これは、これまで取得したデータから、機械学習によって、まだ実験・計算をしていない組成やパラメータに対して予測値と不確かさを見積り、候補点にスコアを付け、最もスコアの良いものを次の実験・計算の対象とするものである。このスコア付けによってより少ない候補点で基準を満たす組成やパラメータを見つける事が可能となる。
ベイズ最適化によって、より少ない回数で最適化問題を解く事が可能になったものの、これを実施するためには各ステップで全ての候補点に対してスコアを付ける必要があるためパラメータが多くなるとその数に比例して計算量が多くなるという問題がある。PHYSBO (optimization tool for PHYSics based on Bayesian Optimization)はPython2で開発されていたベイズ最適化ライブラリCOMBO (COMmon Bayesian Optimization Library)を元に、Python3に対応すると共にスパコン等の高並列環境に対応させたライブラリである。これにより、スーパーコンピュータ等を用いる事で、計算量が多かったスコア計算を高速化している。
研究の内容、成果
PHYSBOを用いる事で、より少ない計算回数、実験回数での物質探索が可能となる。以下には誘電率の大きな材料を見つける問題を例として挙げる。ここでは誘電率の評価に第一原理計算の結果を用いている。(データはA. Takahashi, Y. Kumagai, J. Miyamoto, Y. Mochizuki, F. Oba, Physical Review Materials 4 (2020) 103801のものを使用)物質候補(1277個)の組成を記述子に変換し、これを入力として、ベイズ最適化を実施した結果が図2である。
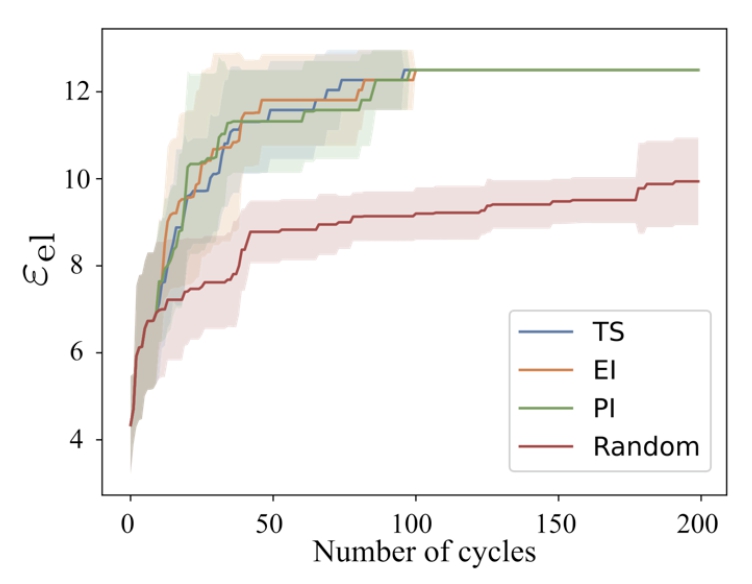
図2: ベイズ最適化の例(横軸はサイクル数、縦軸は誘電率)
ここでは、最初の10回についてはランダムに候補点を選択し、残りのサイクルについてはベイズ最適化(3種類のスコアを比較しており、それぞれTS: Thompson sampling, El: Expected improvement, PI: Probability of improvementを用いた結果である)により候補提案、またはランダム(Random)に候補点を選択した。ベイズ最適化によって、ランダムに実施するよりも少ないサイクル数で高い誘電率の物質が得られる事が分かる。
また、PHYSBOの特徴として複数の候補点を提案する事が可能となっている。下記にその例を示す。
また、PHYSBOの特徴として複数の候補点を提案する事が可能となっている。下記にその例を示す。
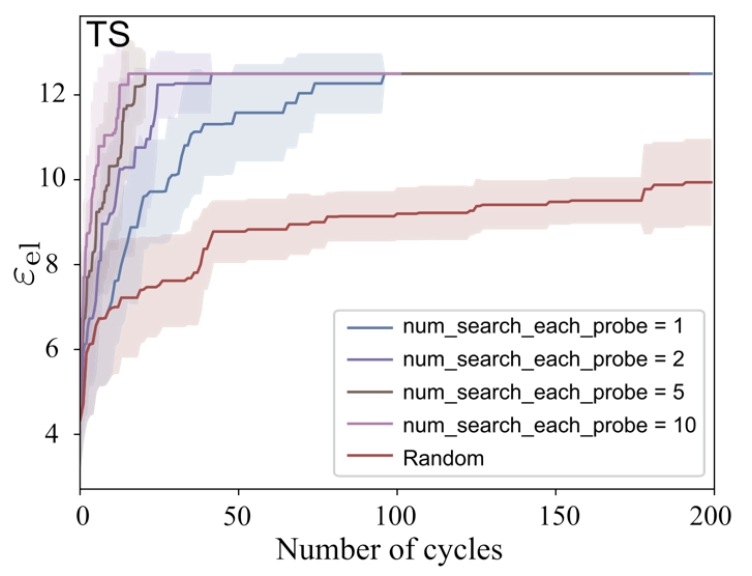
図3: 複数候補の例(横軸はサイクル数、縦軸は誘電率)
ここでは、一回の候補点数が1, 2, 5, 10の例が示されている。一回の候補点を多くする事で、高い誘電率を得るためのサイクル数は少なくなっている。その一方で、必要な計算または実験の合計回数は増える結果となっている。計算または実験が並列処理出来る状況においては全体の時間を短くする事が出来るため有効である。ここで挙げた例のように、PHYSBOを使用する事で、組成や合成パラメータの候補をランダムに選ぶ場合と比較して効率的に探索する事が可能となっている。また、計算や実験が並列処理できる場合にはPHYSBOの機能である複数候補点の提案を利用する事で全体の時間短縮が可能である。
将来への展望
PHYSBOを用いる事で必要な物性から、合成パラメータや組成を探索する最適化問題を効率的に解く事が可能となる。PHYSBOは目的の種類や手法(計算、実験)を問わず広く適用でき、基礎科学における最適化問題を解決するためのツールとしての幅広い活用が期待される。
参考文献
Yuichi Motoyama, Ryo Tamura, Kazuyoshi Yoshimi, Kei Terayama, Tsuyoshi Ueno, Koji Tsuda, Computer Physics Communications 278 (2022) 108405.

